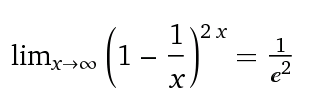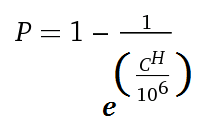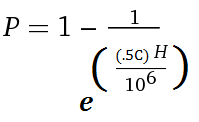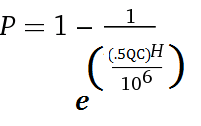Prova matematica che la rete Lightning non può essere una soluzione decentralizzata di scaling Bitcoin

Hai sentito parlare della rete Bitcoin Lightning ? È una proposta che afferma che:

"Utilizzando una rete di questi canali di micropagamento, Bitcoin può scalare fino a miliardi di transazioni al giorno"

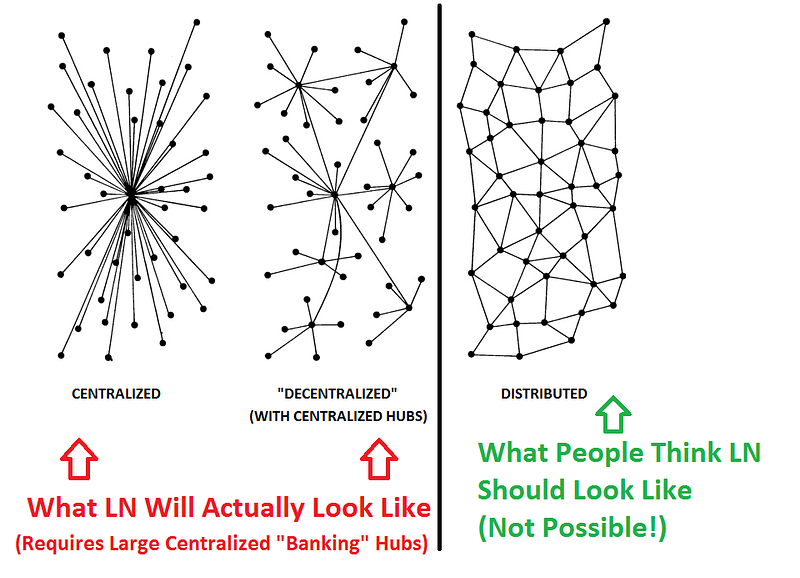
Ciò che non ti dice è che questo può essere realizzato solo utilizzando grandi hub "bancari" centralizzati.

Molti nella comunità Bitcoin hanno erroneamente assunto o sono stati indotti a credere che la rete Lightning (LN) sarebbe una rete distribuita peer-to-peer.

Tuttavia, questo è impossibile. Infatti, anche usando un generoso insieme di ipotesi, dimostreremo che è matematicamente impossibile.

Divideremo questo documento in sezioni. La prima parte sarà una breve panoramica generale del LN. La seconda parte spiegherà in termini semplici perché non può fornire il ridimensionamento decentralizzato. La terza partesarà una prova matematica più rigorosa.

PARTE I: PANORAMICA DELLA RETE DI ILLUMINAZIONE

Il dibattito sul ridimensionamento di Bitcoin

Bitcoin è stato originariamente concepito come denaro peer to peer in grado di scalare con semplici aumenti di blocchi . Tuttavia, la discussione su come ridimensionare la rete è diventata molto più complicata e controversa.

57 Gli sviluppatori di "core" di Bitcoin hanno firmato il loro sostegno a una roadmap di aumento della capacità ufficiale che sostiene la rete Lightning come un "meccanismo di ridimensionamento della larghezza di banda" che può fornire "un decentramento molto alto".

Non siamo d'accordo e dimostreremo che non è così. Dopo aver letto e compreso le informazioni qui, ti consigliamo di trarre le tue conclusioni.

Cos'è la rete Lightning e come funziona?

Lightning Network (LN) è un protocollo che consente una serie di canali di pagamento bidirezionali fuori catena . Ecco un'eccellente serie in 3 parti di Aaron van Wirdum, se vuoi capire i dettagli tecnici.

"Bidirezionale" significa semplicemente due direzioni, così Alice e Bob potrebbero aprire un canale privato e inviare bitcoin avanti e indietro (al di fuori della blockchain):

Per aprire il canale, una o entrambe le parti devono depositare bitcoin in uno speciale indirizzo Bitcoin.¹ Dopo di ciò, possono eseguire tutte le transazioni che vogliono all'interno del canale, fino a quando uno di loro decide di chiuderlo, il che si risolve ( paga i saldi finali appropriati) sulla blockchain principale dei Bitcoin.

Collegamento di più canali

Facendo un passo più in là, se Alice aveva un canale con Bob e Bob aveva anche un canale con Carol, allora Alice poteva inviare indirettamente denaro a Carol: Bob avrebbe prima pagato Carol, e poi Alice avrebbe rimborsato Bob.

The Envisated Network

Gli evangelisti di LN promuovono l'idea che se Alice può pagare Carol attraverso Bob, dovremmo essere in grado di continuare ad estendere questa idea per costruire un'intera rete di canali di pagamento, consentendo così che una grande percentuale di transazioni avvenga fuori catena.

Tuttavia, questo non può essere realisticamente realizzato come una rete peer-to-peer, almeno non di una dimensione significativa.

Semantica "decentrata" contro "distribuita"

Nella conversazione quotidiana su Bitcoin, la maggior parte della gente dice "decentralizzata" per indicare ciò che tecnicamente è una "topologia distribuita".

Viceversa, una rete con hub centralizzati può essere definita tecnicamente "decentralizzata" se non ha un centro singolare.

Ma non lasciarsi prendere dai giochi di parole. Il diagramma qui sotto dovrebbe chiarire le cose:

PARTE II: UNA SPIEGAZIONE PER IL LAYMAN: PERCHÉ LA RETE DI ILLUMINAZIONE NON PU SC SCALARE

Farò questa spiegazione il più breve possibile.

Innanzitutto, devi capire che la rete Lightning non è come le altre reti in quanto non puoi semplicemente connetterti ad un altro utente quando vuoi.

Per inviare o ricevere bitcoin, è necessario un canale di pagamento con quell'utente specifico o una serie collegata di canali di pagamento ( una "route" ).

È inutile creare un canale di pagamento al solo scopo di inviare una transazione fuori catena, poiché richiede una transazione in catena per aprire il canale (e un altro per chiudere). Potresti anche inviare una transazione on-chain; non hai bisogno del LN.

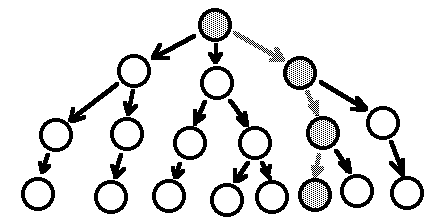
L'idea è che dovresti essere in grado di indirizzare il pagamento verso qualsiasi destinazione attraverso una serie di connessioni. Dal punto di vista di un utente, il percorso potenziale per chiunque altro sembra una struttura ad albero:

Inizia come un problema matematico di base

Assumeremo che l'obiettivo è scalare fino a un milione di utenti.

Pensiamo a questo: se hai un albero con 10 rami e ognuno di questi rami ha 10 foglie, puoi raggiungere 100 foglie.

E se hai un albero con 10 rami, e ognuno ha 10 sotto-rami, e ognuno di quelli a sua volta ha 10 sotto-rami, ecc ... puoi andare su 6 livelli "in profondità" e ottenere: 10 x 10 x 10 x 10 x 10 x 10, o semplicemente: 10⁶, che equivale a un milione.

Dal momento che devi saltare da un ramo all'altro per 6 volte per raggiungere la foglia, possiamo dire che abbiamo "6 luppoli". Quindi sono 10 rami con 6 hop, o nel nostro caso: 10 canali con 6 hop.

Quindi, qual è la sfida?

Il tuo denaro non può essere in due posti allo stesso tempo

Se supponiamo di aver bisogno di 10 canali di pagamento per raggiungere l'intera rete in 6 hop, ciò significa che dovresti dividere i tuoi bitcoin in 10 parti.

Ma probabilmente solo uno di questi canali raggiungerà il destinatario previsto in un dato momento. Ciò significa che potrai inviare solo una parte dei tuoi soldi, ad esempio il 10%.

Potremmo aggirare questo avendo solo 2 canali e, diciamo 20 hop? Torneremo su questa domanda. Per prima cosa, capiamo un altro fatto importante:

Tutti prestano a tutti gli altri

Immagina che Alice voglia inviare 1 BTC a Carol tramite Bob in questo modo: Alice-> Bob-> Carol

Per instradare i soldi , Bob deve avere almeno 1 BTC nel suo "saldo" nel canale con Carol . In sostanza, Alice sta prendendo in prestito da Bob per pagare Carol.

Bob trasferisce il suo 1 BTC a Carol nel canale [Bob-> Carol] e Alice trasferisce 1 BTC a Bob nel canale [Alice-> Bob]. Ecco come funziona -  Alice non può "dare" 1 BTC a Bob per poi passare a Carol.

È davvero un prestito perché la rete utilizza i timelocks per eliminare il rischio di custodia: Alice non può ripagare Bob in sicurezza finché non è sicura che Bob abbia pagato Carol.

In realtà, OGNI hop in rotta verso una destinazione deve disporre dei fondi disponibili per ogni transazione. Quindi, più luppoli vengono utilizzati, più questo onere di prestito viene moltiplicato.

Perché questo è un grosso problema?

Significa che un gran numero di hop è un Deal-Breaker

Diciamo che tutti usavano percorsi con 20 hop e la maggior parte degli utenti spendono circa $ 1000 al mese. Se tutti facessero la loro giusta parte per aiutare a organizzare i pagamenti, ogni utente avrebbe bisogno di instradare $ 20.000 / mese.

Sarebbe anche possibile?

Dipende da molti fattori, tra cui: la quantità di tempo richiesto per un percorso e il numero di transazioni.

Anche se ipotizziamo (probabilmente generoso) che un utente possa instradare 20 volte il suo normale carico di transazioni e subisca solo una riduzione del 50% nella disponibilità dei suoi canali, allora avrebbe bisogno di raddoppiare il numero di canali che normalmente avrebbe.

Nella realtà, è ancora peggio

Ci sono almeno 5 ulteriori problemi che peggiorano la situazione.

1. Anche la matematica di base con cui abbiamo iniziato: 10⁶ = 1.000.000 non è del tutto applicabile. Se supponiamo che i pari formino per lo più connessioni casuali senza un'autorità centrale per pianificare i percorsi, allora c'è una certa probabilità di successo. Una possibilità su un milione, ripetuta un milione di volte, produce solo un tasso di successo del 63%. La scelta di 2 milioni di volte migliora l'84%, il che significherebbe aumentare il numero di canali.³
2. Mentre gli utenti spendono il loro reddito, le rotte disponibili si degradano, fino al momento in cui più fondi vengono depositati. In altre parole, quando una persona riceve un pagamento di stipendio e deposita fondi nella rete, i suoi canali sono al massimo, con pieno potere di routing. Ma mentre i loro soldi vengono spesi, questo potere scende verso lo zero. Mediato, questo modello riduce la potenza di routing di circa la metà, richiedendo il doppio del numero di canali.
3. I fondi di routing per gli altri interrompono una distribuzione uniforme di fondi, il che riduce anche il numero di canali utilizzabili.
4. C'è una grande disparità di ricchezza in ogni popolazione. Pertanto, il numero di utenti che possono instradare i fondi per qualsiasi altro utente casuale è solo una frazione della rete. E questo problema è amplificato in modo esponenziale con un numero crescente di luppolo.
5. Esiste sempre il rischio che un canale di routing non risponda (intenzionalmente o involontariamente). Questo rischio aumenta anche in modo esponenziale con un numero crescente di luppolo.

Il riepilogo "TLDR"

Per raggiungere chiunque in una grande rete con una serie di connessioni di canali ramificati, è necessario un numero elevato di canali o un numero elevato di hop.

Entrambi sono un grosso problema. Un gran numero di canali significa che gli utenti devono dividere i loro fondi e non possono fare altro che piccoli acquisti. E un gran numero di hop significa che i soldi di tutti saranno vincolati a instradare i soldi di tutti gli altri.

Conclusione: un sistema completamente non lavorabile

Poiché la rete raggiunge un milione di utenti, sembra che non ci sarà un modo realistico per evitare questi problemi. Dividere i fondi in molti canali e prestare continuamente denaro rende la rete inutilizzabile.

Le uniche visioni concepibili sono A) tutti depositano MOLTO molto di più di quanto non debbano negoziare, o B) il sistema dipende da grandi hub centralizzati.

Né è una soluzione di ridimensionamento decentralizzato, o addirittura una parte importante di uno.

PARTE III: PROVA MATEMATICA INFORMALE

1. Presupposti

Modellare una rete teorica che in realtà non esiste, di un grande gruppo di persone diverse, è ovviamente impossibile da fare con precisione. Riconosciamo di fare una serie di ipotesi, alcune affermate, alcune implicite e alcune generose per i critici di questa dimostrazione.

In questo contesto, miriamo a dimostrare, attraverso calcoli di probabilità, che sarà necessario un gran numero di canali di pagamento aperti per ciascun utente, rendendo così il sistema sostanzialmente inutilizzabile a una dimensione di 1.000.000 di utenti.

2. Canali e luppolo necessari, senza vincoli

Modellando la rete come un grafico complesso di 1.000.000 nodi, esamineremo la probabilità di raggiungere un peer casuale dato un certo numero di canali aperti, C , e consentendo un certo numero di salti, H .

Dal punto di vista di un utente, il raggiungimento di colleghi distanti attraverso una serie di canali di diramazione è simile alla struttura ad albero. ⁴ Il numero di foglie cresce in modo esponenziale e sono possibili destinazioni di transazione.

Per semplificare i calcoli, ignoreremo la possibilità che un ramo sull'albero possa collegarsi a un altro ramo già sull'albero (come un antenato o un cugino).

Questa possibilità potrebbe ridurre il numero di peer trovati da una ramificazione puramente esponenziale a un numero leggermente inferiore. Poiché stiamo tentando di dimostrare che un numero relativamente basso di pari potrebbe essere raggiunto senza un gran numero di canali o di luppolo, e il numero reale sarebbe ancora più basso, si tratta di un presupposto generoso (rafforzamento della dimostrazione).

Lasciare n è il numero di fogli, definito come C ^ H . Ad esempio, 10 canali aperti e 6 hop sono 10⁶ = 1.000.000.

La probabilità P per non aver scelto un membro di un set | N | con cardinalità n campionando n volte, con la sostituzione è:

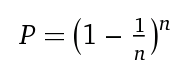
(Nel nostro caso, ottenendo una destinazione desiderata abbinandola a una foglia.)

Possiamo generalizzare questo con la forma limitante:

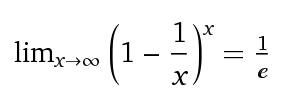
Poiché 1 / e = 0,3678 ... allora la probabilità di scegliere correttamente almeno una volta è (1- (1 / e)) = 63.21 ...%

Avere accesso a un dato peer ad un tasso di solo il 63,21% è troppo basso per essere considerato successo per un sistema di pagamento.

L'utilizzo di un numero diverso di prove può essere espresso come:

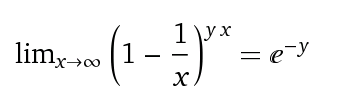
Per esempio:

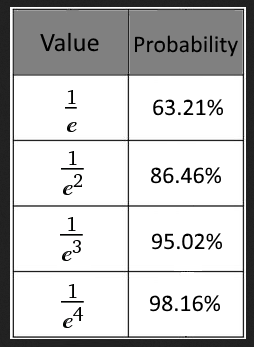
Prendendo vari esponenti di e , possiamo calcolare le probabilità corrispondenti:

Usando un valore di 1.000.000 di utenti e il modulo limitante, ricaviamo la formula:

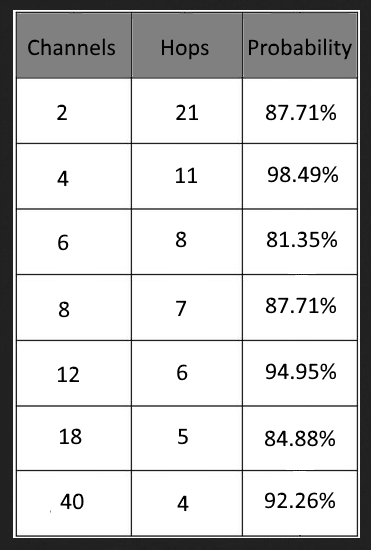
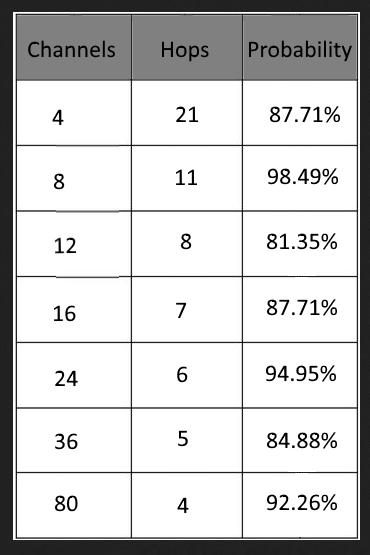
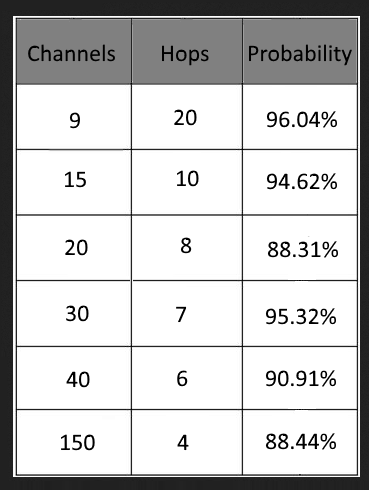
Usando questa formula, possiamo calcolare alcuni valori iniziali che raggiungono almeno il livello di probabilità dell'80%; tuttavia questo non sta considerando altri fattori non ancora discussi:

1

3. Canali e luppolo richiesti, con un vincolo di base di denaro

Tutto il luppolo lungo il percorso deve disporre di fondi sufficienti per elaborare qualsiasi pagamento che desiderano servire. Questo è il vincolo di denaro.

La modellazione di una rete di un milione di utenti con un'ampia varietà di profili finanziari e modelli di spesa non è possibile farlo proprio perché ci sono troppi fattori sconosciuti.

Tuttavia, possiamo formulare un'ipotesi molto generica sul senso comune che molti o la maggior parte degli utenti riceveranno un qualche tipo di reddito in una sorta di intervallo regolare e depositeranno una detrazione di fondi nella LN per la spesa.

I fondi depositati saranno generalmente spesi o eventualmente ritirati. (Supponiamo che LN non venga utilizzato come veicolo di risparmio)

Man mano che gli utenti spendono fondi, la disponibilità dei canali di pagamento per il routing si ridurrà, sia perché un canale si chiude, sia perché l'importo finanziato diminuisce. Quando vengono depositati fondi aggiuntivi, le capacità di routing sono rivitalizzate.

Non disponiamo di un modello dettagliato e di quanti utenti vengono pagati quanto, quando e quanto spesso. Tuttavia, possiamo aggregare il comportamento del gruppo di utenti grazie alla legge dei grandi numeri, che afferma che "la media dei risultati ottenuti da un numero elevato di prove dovrebbe essere vicina al valore atteso".

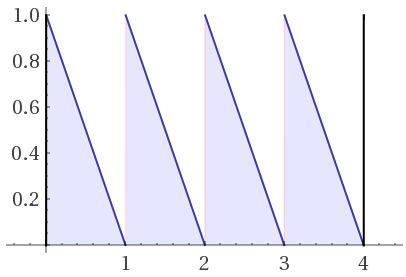
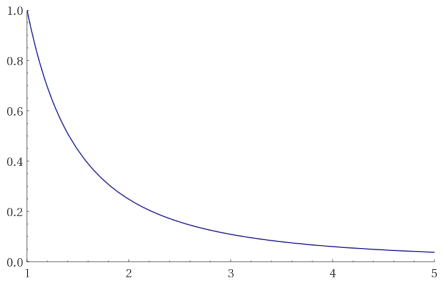
I cicli tipici dei consumatori consistono nel ricevere reddito, spenderlo e poi ripetere. Possiamo generalizzare questo comportamento come un'onda inversa a dente di sega:

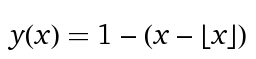
Visivamente, appare come:

I pagamenti di stipendio sono rappresentati da picchi, e il reddito viene poi speso gradualmente fino al pagamento successivo.

L'integrazione della funzione dimezza il valore del periodo, come previsto:

Ciò è anche evidente dal punto di vista visivo poiché le onde formano triangoli rettangoli che tagliano metà dell'area.

L'implicazione è che circa la metà dei canali che verrebbero utilizzati per il routing non sono validi. Pertanto, il numero di canali per ciascun salto deve essere raddoppiato.

La nostra formula di probabilità cambia in:

E la nostra tabella dei risultati diventa:

C'è anche un'enorme generosa ipotesi che stiamo facendo , ovvero che tutti gli utenti sono una parte utile del set di partecipanti al routing per tutti gli altri utenti. In realtà, una distribuzione della ricchezza molto disomogenea probabilmente imporrà ulteriori e significativi vincoli al sistema.

4. Vincolo aggiuntivo di prestito

Oltre agli oneri derivanti dalla divisione dei fondi e dalla ricerca di rotte, assumiamo che l'utente partecipi anche alla rete aiutando gli altri a instradare i pagamenti.

Questo disturba l'utente in due modi.

In primo luogo, potrebbe causare una squilibrata distribuzione dei fondi personali dell'utente, diminuendo il numero di rotte disponibili. Nel corso del tempo, questo potrebbe teoricamente fare una media con il denaro che scorre in entrambe le direzioni di un dato canale. Tuttavia, ogni utente sarebbe soggetto ad un ampio grado di varianza in qualsiasi momento.

Il secondo è che il denaro utilizzato per instradare i pagamenti degli altri non è disponibile per l'utente durante il periodo in cui la rotta è in uso.

Noi ignoreremo generosamente la prima causa di rottura e tenteremo solo di modellare il secondo. Adotteremo l'approccio semplicistico ipotizzando che tutti gli utenti abbiano lo stesso numero medio di transazioni e di volume di spesa e assumiamo che ogni utente partecipi in modo uguale al routing.

Definiamo le seguenti variabili:

U: il numero di utenti
H: il numero di hop
V : il volume totale della transazione di rete durante un periodo di tempo
v: il volume della transazione per utente durante un periodo di tempo 
r : il volume totale instradato per utente durante un periodo di tempo 
D : la durata in ore di un periodo di tempo
t : numero medio di transazioni per utente per il periodo D 
d: la durata in ore del percorso medio

Poiché ciascun hop deve instradare l'intero importo della transazione per qualsiasi transazione in un percorso a cui partecipa, il volume totale indirizzato per l'intera rete durante un periodo di tempo = VH.

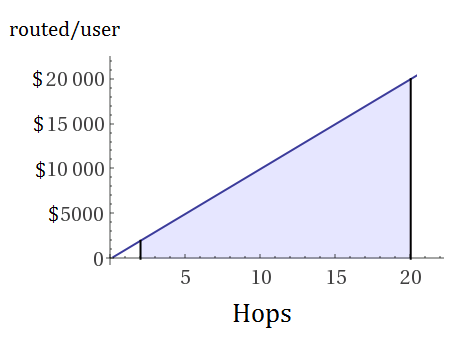
Quindi, r = VH / U. E poiché V / U = v, r = Hv .

Ad esempio, se v = $ 1000, il grafico appare come:

Cerchiamo di introdurre il concetto di dollaro per misurare la capacità di routing.

Naturalmente, ogni utente può spendere i propri soldi solo una volta. Ma allo scopo di instradare il denaro degli altri, possiamo pensare alle ore in dollari come il totale dei dollari nei loro canali, moltiplicato per il numero di ore disponibili. Ad esempio, $ 1000 seduti immobili per una settimana sono 168.000 dollari-ora.

Possiamo quindi calcolare un quoziente Q, che rappresenta la percentuale di capacità disponibile rimanente dopo il routing per gli altri:

Q = 1- ( d ( H -1)) / D

Si noti che v e t non compaiono nell'equazione in quanto sono scomposti, ma sono impliciti nel rapporto d / D. Il motivo per H -1 è che un hop non costa alla rete nulla oltre le transazioni di un utente ( r = Hv ).

Ad esempio, se la rete utilizza 4 hop e le route richiedono 4 ore e i saldi dell'utente per il routing si basano su 168 ore (1 settimana), quindi:

Q = 1- ((4) * (3)) / 168) = 0,92

La nostra formula di probabilità è ora:

Supponendo D = 168 e tempo di instradamento d = 4 ore, arriviamo alle seguenti probabilità:

5. Determinazione dei limiti di transazione in base a una distribuzione di Pareto

Sembra appena necessario dimostrare che se i fondi devono essere suddivisi in piccoli contenitori, ci sarebbe un enorme effetto negativo sull'usabilità. Tuttavia, per completezza, abbiamo incluso questa sezione.

Presumiamo che la maggior parte della spesa per consumi e imprese segue una distribuzione di Pareto in quanto ciascun utente effettua un numero relativamente piccolo di transazioni di grandi dimensioni, diverse transazioni di medie dimensioni e una quantità maggiore di transazioni minori.

La funzione di densità di probabilità di Pareto è espressa come:

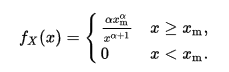
Per la curva Pareto di tipo 1 più semplice, questo semplifica:

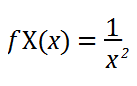
La distribuzione non cambia applicando le costanti, ma possiamo immaginare meglio il modello con alcuni valori del mondo reale moltiplicando i valori y per 1000, in modo che le quantità in dollari per i grandi oggetti diventino sostanziali e si integrino su un tipico insieme di valori x ( numero di transazioni per ciascun valore in dollari), ad esempio 50.

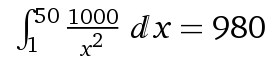
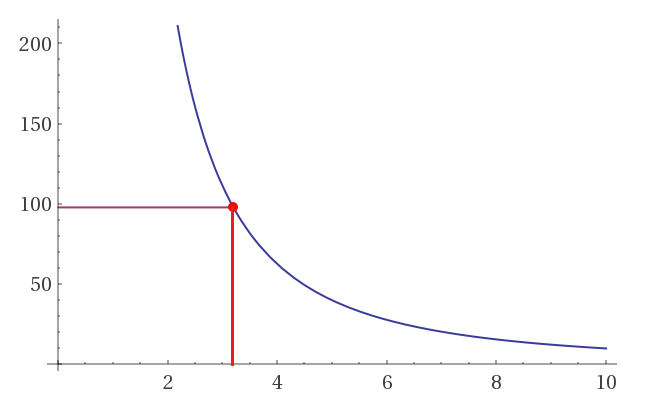
La somma totale delle transazioni = $ 980. Usando un valore del 10% di $ 98,  
possiamo risolvere l'equazione: 98 = 1000 / x² per ottenere 3.194 transazioni.

Successivamente, integreremo il più piccolo insieme di transazioni per ottenere il valore di somma delle transazioni che hanno importi inferiori al nostro valore minimo di $ 98:

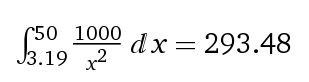
Dal 293.48 / 980 = .299, possiamo dire che solo il 29,9% di tutta l'attività economica desiderata sarebbe possibile se venissero usati 10 canali.

Pensieri finali

Mi aspetto che i critici facciano il pignolo. Ti incoraggio a fare il tuo pensiero critico. Non dimenticare le generose ipotesi che abbiamo fatto per ignorare la disparità di ricchezza.

Ricorda, Bitcoin deve essere decentralizzato. Diffida della razionalizzazione di "La centralizzazione è ok fintanto che lo strato di base viene mantenuto decentralizzato". Questa è una trappola insidiosa che consente di forzare gli utenti a uscire dallo strato di base e nei sistemi centralizzati. Non dobbiamo mai permetterlo.

Quindi, Bitcoin è in difficoltà perché le soluzioni di secondo livello potrebbero non funzionare? No, per niente. Bitcoin è stato progettato per scalare on-chain con aumenti di blocchi semplici. Può farlo e lo farà, se lo permettiamo.

appendice

Ho pubblicato un breve follow-up su alcuni fraintendimenti e obiezioni.

Aggiornamento 7 giugno 2018

Le previsioni di questo articolo si stanno dimostrando corrette visto che stiamo già vedendo il modulo di rete in hub centralizzati. La narrativa dei sostenitori di LN si sta ora spostando verso "ok centralizzata ma non preoccuparti". Per sapere perché gli hub centralizzati portano alla censura economica, clicca qui.

Le note

1. Non un nuovo tipo di indirizzo. Semplicemente, un indirizzo multi-firma per gli scopi del canale.
2. Originariamente pubblicato da Carl S. Sterner in 'Resilienza e decentramento'.
3. Ci sono ulteriori considerazioni sulla probabilità come discusso nella parte III.
4. Tecnicamente un grafico complesso, non una struttura ad albero, sebbene l'albero sia un costrutto mentale appropriato. Avremmo potuto usare calcoli di teoria del grafico più sofisticati (forse la formula della somma dei gradi o una formula correlata) per arrivare a un numero più preciso di nodi raggiunti con D gradi ed E , ma abbiamo deciso che non era necessario perché il numero massimo di nodi è usato, che è un'ipotesi generosa.
5. 
   
6. https://medium.com/@jonaldfyookball/mathematical-proof-that-the-lightning-network-cannot-be-a-decentralized-bitcoin-scaling-solution-1b8147650800